Microbenchmarks
Latency and Throughput of MPX Instructions
The following table shows the latency-throughput results of Intel MPX instructions. For this evaluation, we extended the scripts used to build Agner Fog’s instruction tables.1 Our scripts can be downloaded here.
| Instruction | μops2 | Tput | Lat | P03 | P13 | P23 | P33 | P43 | P53 | P63 | P73 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
bndmk b, m1 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | |||||
bndcl b, m1 | 2 | 1 | 1 | 0.5 | 1 | 0.5 | ||||||
bndcl b, r | 1 | 2 | 1 | 1 | 1 | |||||||
bndcu b, m1 | 2 | 1 | 1 | 0.5 | 1 | 0.5 | ||||||
bndcu b, r | 1 | 2 | 1 | 1 | 1 | |||||||
bndmov b, m | 3 | 1 | 1 | 1 | 1 | 1 | ||||||
bndmov b, b | 2 | 2 | 1 | 1 | 1 | 1 | 1 | |||||
bndmov m, b | 5 | 0.5 | 2 | 0.5 | 0.3 | 0.3 | 1 | 0.3 | ||||
bndldx b, m | 8 | 0.4 | 4-6 | 0.4 | 0.5 | 0.9 | 0.9 | 0.3 | 0.4 | |||
bndstx m, b | 8 | 0.3 | 4-6 | 0.3 | 0.5 | 0.5 | 1 | 0.4 |
1 - Here m means LEA-like address calculation and not memory access!
2 - μops is short for number of microoperations per instruction.
3 - Denotes the number of microoperations executed on the port per each cycle. It can be interpreted as port usage.
In our extension, we wrote a loop with 1,000 copies of an instruction under test and run the loop 100 times. This gives us 100,000 executions in total. We run each experiment 10 times to make sure the results were not influenced by external factors. For each run, we initialize all BND registers with dummy values to avoid interrupts caused by failed bound checks.
Note 1: bndcu has a one’s complement version bndcn, we skip it for clarity.
Note 2: Ideally, we would measure latency for the serial case. However, we were not able to create a data dependency for MPX instructions. Therefore, we resorted to estimating latency based on our microbenchmarks and Intel documentation (i.e., it is our educated guess).
Note 3: For our Skylake, ports P0, P1, P5, and P6 are arithmetic/logic units, P2 and P3 are load and address-generation units, P4 is a store unit, and P7 is load/store address-generation unit.
Let us look at bndmk b, m first. The instruction creates bounds based on the m second operand and puts them in a b bounds register (note that m in this case is not an actual memory access, but a LEA-like expression). Each bndmk instruction is split into two micro-operations (μops). In one cycle, two bndmks can be executed in parallel, i.e., throughput is 2. This also implies there are four μops per cycle: two μops of one bndmk are executed in parallel on P0 and P1, and two other μops of another bndmk—on P5 and P6. The ports’ columns show their utilization; in this case, P0, P1, P5, and P6 are 100% utilized. Note how P2-P4—ports to access memory—are not used by this instruction. Finally, the latency of bndmk is one cycle since two μops can be executed in parallel.
For another example, consider bndcl b, m. Its throughput is only one instruction/cycle, and the bottleneck is P1. P0 and P7 have only 50% utilization, i.e., they execute one μop in one cycle and then stall for another cycle, waiting for P1. Note how bndcl b, r version of the same instruction achieves two instructions/cycle because it does not use P1.
Final example is bndldx b, m. The instruction loads bounds into b from a memory location derived from address m (from a bounds table). This complex instruction is composed of 8 μops occupying 6 ports and has a low throughput of around 0.4 instructions/cycle (Storing bounds in memory explains why it is so complicated). We estimate the latency of bndldx as taking 4 to 6 cycles, with a bottleneck of loading from memory (ports P2 and P3). Moreover, since it uses most of the available ports, it may hinder scalability when hyperthreading is used.
In general, most operations have latencies of one cycle, e.g., the most frequently used bndcl and bndcu. The serious bottleneck is storing/loading the bounds with bndstx and bndldx since they undergo a complex algorithm of accessing bounds tables.
Overhead of MPX checks
In our experiments, we observed that MPX protection does not increase the IPC (instructions/cycle) of programs, which is usually the case for memory-safety techniques (see our IPC evaluation). This was surprising: we expected that MPX would increase IPC of programs with low original IPC, i.e., it would take advantage of the underutilized CPU resources.
To understand what causes this bottleneck, we measured the throughput of typical MPX check sequences using the same framework as above. We originally blamed an unjustified data dependency between bndcl, bndcu, and the protected memory access; this speculation turned out to be incorrect.
Here are the throughput measurements:
| Check sequence | Mem access | IPC | Comments | |
|---|---|---|---|---|
load | 2 | native program, no checks | ||
bndcl r + | load | 4 | single-bound check, very rare | |
bndcl m + | load | 2 | single-bound check, very rare | |
bndcl r + bndcu r + | load | 3 | both-bounds simple check, rare | |
bndcl m + bndcu m + | load | 1.5 | both-bounds LEA-style check, frequent | |
store | 1 | native program, no checks | ||
bndcl r + | store | 2 | single-bound check, very rare | |
bndcl m + | store | 2 | single-bound check, very rare | |
bndcl r + bndcu r + | store | 3 | both-bounds simple check, rare | |
bndcl m + bndcu m + | store | 1.5 | both-bounds LEA-style check, frequent |
Note: It is crucial to distinguish two types of operands used in bounds checking: direct memory address (r or register operand) and relative LEA-style addresses(m or memory operands). In assembly, the first one looks like this: bndcl %rax,%bnd0—it takes the address in rax, compares it with the lower bound of bnd0 and rises a #BR exception if it violates the bound. This instruction consist of one comparison and maps to a single micro-operation. The second type is more complex: bndcl (%rax,%rbx,4),%bnd0. First, the address has to be calculated by multiplying rbx by 4 and then adding rax. Only afterwards can the resulting address be checked against the lower bound of bnd0. Accordingly, it requires one more micro-operation to calculate the address and, as we can see from the table in the previous section, it can be executed only on port 1.
The table highlights a bottleneck of bndcl m and bndcu m (due to contention on port P1). Let’s first consider checks before loads and then before stores.
In case of loads, the original program can execute two loads in parallel, achieving a throughput of 2 IPC (note that the loaded data is always in a Memory Ordering Buffer). Under MPX, the load can be prepended with a single-bound check—which can happen in case of loop optimizations, but is very rare in reality. If this single-bound check is bndcl r, then IPC doubles: two loads and two bounds-checks can be executed in parallel because they do not share ports. However, if the check is bndcl m, then IPC stays the same (two): only one load and one bounds-check can execute in one cycle since bndcl m contends on P1. The typical case is when MPX inserts two bounds checks. In this case, for r checks, IPC increases to three instructions per cycle: one load, one lower-, and one upper-bound check per cycle. For m checks, IPC becomes less than the original: two loads and four checks are scheduled in four cycles, thus IPC of 1.5. These scenarious are illustrated by the following figure:

The similar analysis applies for stores. However, the original IPC in this case is one store per cycle, which means that any variant of MPX checks increases IPC.
In summary, since loads usually dominate memory accesses, and both-bounds checks dominate MPX instrumentation, the final IPC is around 1.5-3. In comparison to original IPC of 2 loads/cycle, the MPX-protected program has approximately the same IPC.
As our performance measurements show, it causes major performance degradation. It can be fixed, however; if the next generations of CPUs will provide the relative memory address calculation on other ports, the checks could be parallelized and performance will improve. We can speculate that GCC-MPX could reach the results of AddressSanitizer in this case, because the instruction overheads are similar. Accordingly, ICC version would be even better and the slowdowns might drop lower than 20%. But we must note that we do not have any hard proof for this speculation.
OS Bounds Tables Overhead
Intel MPX relies on the operating system to manage special Bounds Tables (BTs) that hold pointer metadata. To illustrate the additional overhead of allocating and de-allocating BTs, two microbenchmarks showcase the worst case scenarios. The source code for them can be found here.
The first microbenchmark stores a large set of pointers in such memory locations that each of them will have a separate BT, i.e., this benchmark indirectly creates a huge amount of bounds tables. The second one does the same, but additionally frees all the memory right after it has been assigned, thus triggering BT de-allocation.
The characteristics of microbenchmarks:
- working with 3,000 BTs
- average over 10 runs
- compilation flags:
- native version:
-g -O0 - MPX version:
-mmpx -fcheck-pointer-bounds -lmpx -lmpxwrappers -g -O0
- native version:
Note that we disabled all compiler optimizations to showcase the influence of OS alone.
The following table shows the impact of OS managing BTs, i.e., overheads of MPX version in performance and number of instructions w.r.t. native.
| Perf | Instr in user space | Instr in kernel space | |
|---|---|---|---|
| Only allocation | 2.33× | 7.5% | 160% |
| Allocation and de-allocation | 2.25× | 10% | 139% |
In both cases, most of the runtime parameters (cache locality, branch misses, etc.) of the MPX-protected version are equivalent to the native one. However, the performance overhead is noticeable – more than 2 times. It is caused by a single parameter that varies – the number of instructions executed in the kernel space. (Note how the number of instructions executed in the user space increases only slightly.) It means that the overhead is caused purely by the BT management in the kernel.
We conclude that OS can account for performance overhead of 2.3× in the worst case.
More statistics collected can be found here: os_microbenchmark.md.
Performance microbenchmarks
Below are the four microbenchmarks, each highlighting a separate MPX feature:
- arraywrite: writing to memory (stress
bndclandbndcu) - arrayread: reading from memory (stress
bndclandbndcu) - struct: writing in an inner array inside a struct (the bounds-narrowing feature via
bndmkandbndmov) - ptrcreation: assigning new values to pointers (stress
bndstx)
All microbenchmarks were compiled with -O2 optimizations.
Performance results:
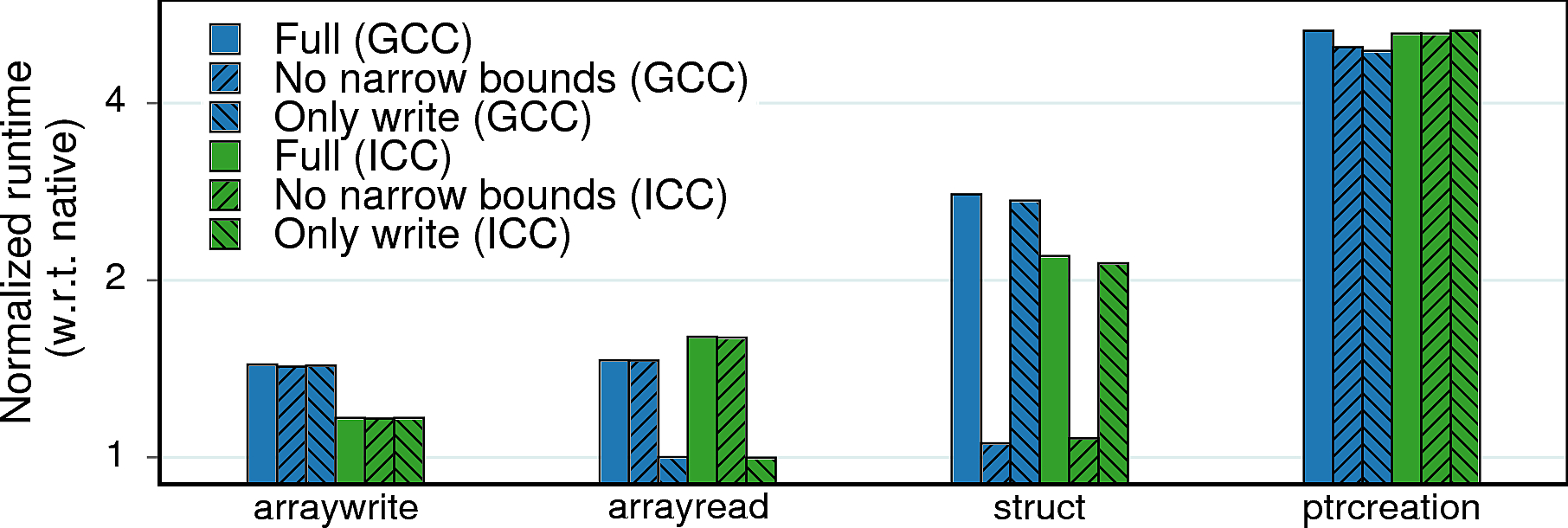
Observation 1: arraywrite and arrayread represent the bare overhead of bounds-checking instructions (all in registers), 50% in this case. struct has a higher overhead of 2.1−2.8× due to the more expensive making and moving of bounds to and from the stack. 5× overhead of ptrcreation is due to storing of bounds – the most expensive MPX operation.
Observation 2: There is a 25% difference between GCC and ICC in arraywrite. This is the effect of optimizations: GCC’s MPX pass blocks loop unrolling while ICC’s implementation takes advantage of it. (Interestingly, the same happened in case of arrayread but the native ICC version was optimized even better, which led to a relatively poor performance of ICC’s MPX.)
Observation 3: The overhead of arrayread becomes negligible with the only-writes MPX version: the only memory accesses in this benchmark are reads which are left uninstrumented. The same logic applies to struct – disabling narrowing of bounds effectively removes expensive bndmk and bndmov instructions and lowers performance overhead to a bare minimum.
Raw results can be found in the repository.
Multithreading microbenchmark
Intel MPX has fundamental problems with multithreading support. In a nutshell, the problem arises because of the non-atomic way MPX loads and stores pointer bounds via its bndldx and bndstx instructions whenever a real pointer is loaded/stored from/to memory. More information is provided in our paper2 and in other sources3.
We constructed two test cases that break MPX in a multithreaded environment: one that leads to a false positive (false alarm) and one that leads to a false negative (undetected real bug). The test cases roughly work as follows; see our paper for more details. A “pointer bounds” data race happens on the arr array of pointers. The background thread fills this array with all pointers to the first or to the second object alternately. Meanwhile, the main thread accesses a whatever object is currently pointed-to by the array items. Note that depending on the value of the constant offset, the original program is either always-correct or always-buggy: if offset is zero, then the main thread always accesses the correct object, otherwise it accesses an incorrect, adjacent object.
The test cases are compiled and run as follows:
- false negative:
- source code
- compile at
-O1to have simple non-vectorized asm - run with
CHKP_RT_MODE=count CHKP_RT_PRINT_SUMMARY=1 CHKP_RT_VERBOSE=0 ./gcc_mpx/multithreading_fn - Results:
- in correct MPX implementation, output must be 10,000,000 (
ITERATIONS*MAXSIZE) - in current GCC and ICC implementations, output is less than 10,000,000 (due to broken multithreading)
- in correct MPX implementation, output must be 10,000,000 (
- false positive:
- source code
- compile at
-O1to have simple non-vectorized asm - run with
CHKP_RT_MODE=count CHKP_RT_PRINT_SUMMARY=1 CHKP_RT_VERBOSE=0 ./gcc_mpx/multithreading_fp - Results:
- in correct MPX implementation, no
#BRexception must be output - in current GCC and ICC implementations, output is
#BRexception nondetermenistically (due to broken multithreading)
- in correct MPX implementation, no
Note: Make sure the test cases run on two cores!
We must note that the test cases do not conform to the memory model introduced in C11 and C++11 standards. Under C11, this code by itself has undefined behavior, and the compilers are free to produce a potentially misbehaving program. Thus, the discussion above applies only to legacy C/C++ code where the data race is technically allowed. Under the new C11 thread model, arr must be declared as an array of atomic pointers. Ideally, the compiler would recognize loads/stores of atomic pointers and enclose them and their corresponding bounds loads/stores in a critical section. Unfortunately, our investigation proved that current compilers do not generate correct code neither with GCC-specific __atomic_store() nor with C11-defined _Atomic types.